Vectors for Physics Formulas

Vectors for Physics and Math

In this Vectors Physics and Math tutorial you will learn vectors definition, Types of Vector, Triangle Law of Vector Addition of Two Vectors, Parallelogram Law of Vector Addition, Polygon Law of Vector Addition, vector subtraction, Resolution of Vector Into Components, scalar multiplication (Dot Product), vector multiplication (Cross Product), vector algebra, Lami's Theorem, Relative Velocity, concepts for finding vectors with some vector examples and illustrations. Vector is one of the most important topics for Physics and mathematics

Types of Vector

(1) Equal vectors : Two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ are said to be equal when they have equal magnitudes and same direction.

(2) Parallel vectors : Two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ are said to be parallel when
(i) Both have same direction.
(ii) One vector is scalar (positive) non-zero multiple of another vector.

(3) Anti-parallel vectors : Two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ are said to be anti-parallel when
(i) Both have opposite direction.
(ii) One vector is scalar non-zero negative multiple of another vector.

(4) Collinear vectors : When the vectors under consideration can share the same support or have a common support then the considered vectors are collinear.

(5) Zero vector $(\overrightarrow{0})$: A vector having zero magnitude and arbitrary direction (not known to us) is a zero vector.

(6) Unit vector : A vector divided by its magnitude is a unit vector. Unit vector for $\overrightarrow{A}$ is $\hat{A}$ (read as A cap or A hat).
Since, $\hat{A}=\frac{\overrightarrow{A}}{A}$ $\Rightarrow $$\overrightarrow{A}=A\,\hat{A}$.
Thus, we can say that unit vector gives us the direction.

(7) Orthogonal unit vectors $\hat{i}\,,\,\hat{j}$ and $\hat{k}$are called orthogonal unit vectors. These vectors must form a Right Handed Triad (It is a coordinate system such that when we Curl the fingers of right hand from x to y then we must get the direction of z along thumb).

Triangle Law of Vector Addition of Two Vectors

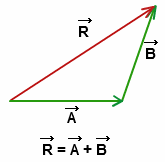
If two non zero vectors are represented by the two sides of a triangle taken in same order then the resultant is given by the closing side of triangle in opposite order. i.e.$\overrightarrow{R}=\overrightarrow{A}+\overrightarrow{B}$
 $\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$

Parallelogram Law of Vector Addition

If two non zero vectors are represented by the two adjacent sides of a parallelogram then the resultant is given by the diagonal of the parallelogram passing through the point of intersection of the two vectors.

Polygon Law of Vector Addition

Vector Subtraction